Binomial Determinants for Tiling Problems

Yield to the Holonomic Ansatz

Project maintained by wongey Hosted on GitHub Pages — Theme by mattgraham

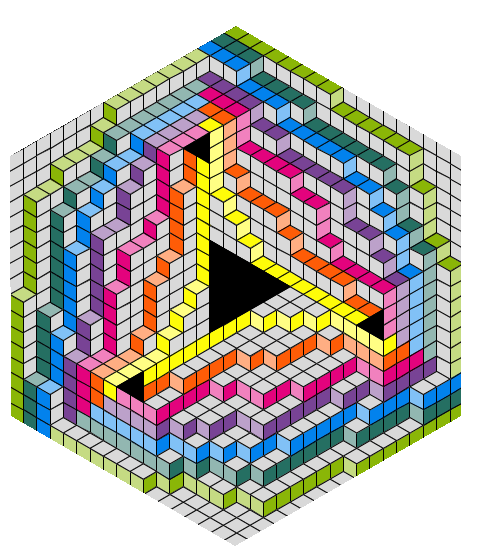
We present and prove closed form expressions for some families of binomial determinants with signed Kronecker deltas that are located along an arbitrary diagonal in the corresponding matrix. They count cyclically symmetric rhombus tilings of hexagonal regions with triangular holes. We extend a previous systematic study of these families, where the locations of the Kronecker deltas depended on an additional parameter, to families with negative Kronecker deltas. By adapting Zeilberger’s holonomic ansatz to make it work for our problems, we can take full advantage of computer algebra tools for symbolic summation. This, together with the combinatorial interpretation, allows us to realize some new determinantal relationships. From there, we are able to resolve all remaining open conjectures related to these determinants, including one from 2005 due to Lascoux and Krattenthaler.

Authors

Paper

Files

Past and Upcoming Talks

All times are CEST.